Robotics Perception
课程链接:https://www.coursera.org/learn/robotics-perception/
Week 1
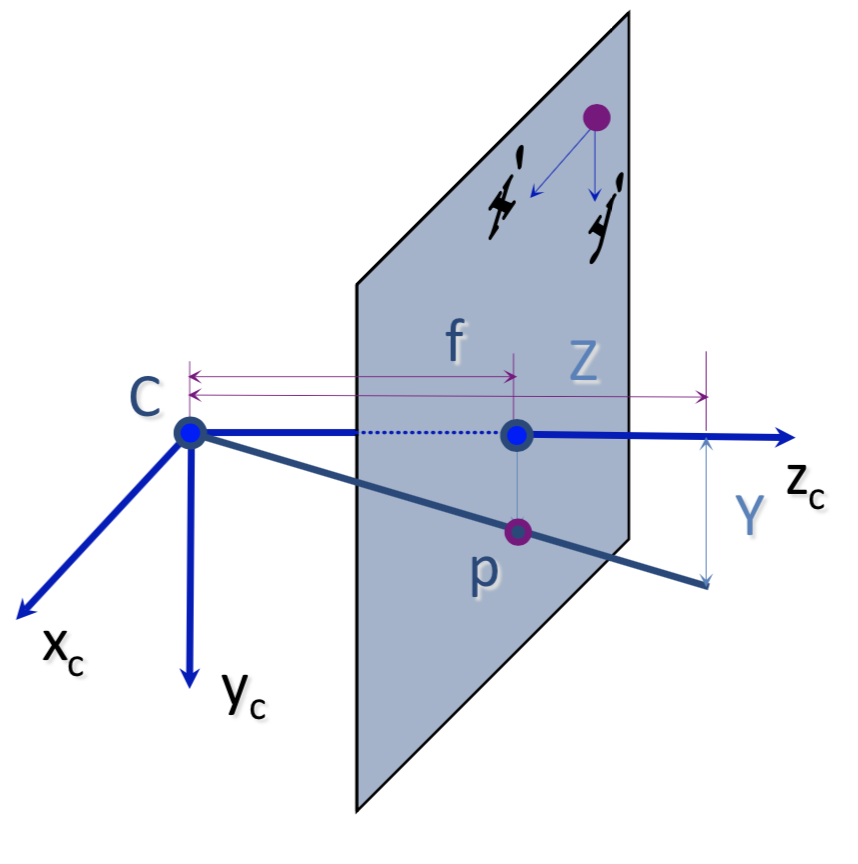
Pinhole Model
Assuming image plane is in front of the lens
\[ y=f\dfrac{Y}{Z} \]
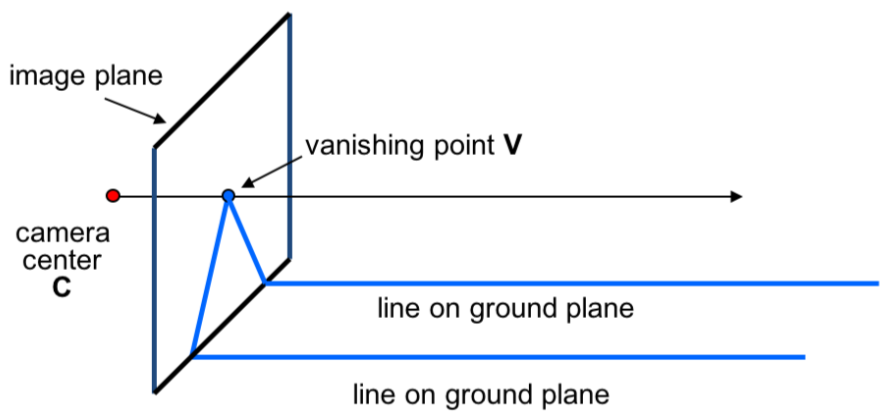
Vanishing Points
- Any two parallel lines have the same vanishing point
- The ray from C through v point is parallel to the lines
- An image may have more than one vanishing point
Vanishing Lines
- Any set of parallel lines on the plane define a vanishing point
- The union of all of these vanishing points is the horizon line (also called vanishing line)
- Note that different planes define different vanishing lines
Point and Line Duality
- Line: \(l = x \times x'\)
- Point: \(x = l \times l'\)
- Points and lines are dual in projective space: given any formula, can switch the meanings of points and lines to get another formula
Point at Infinity
Line \(l = (a, b, c)^T\) intersects at \((b, -a, 0)^T\).
Perspective Projection
1. Camera Projection Matrix
\[ Z_{c} \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \left[ \begin{array}{ccc|c} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right] \left[ \begin{array}{c} X_c \\ Y_c \\ Z_c \\ 1 \\ \end{array} \right] \]
2. Intrinsic Camera Parameters
\[ \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \left[ \begin{array}{ccc} \alpha_{x} & s & p_{x} \\ 0 & \alpha_{y} & p_{y} \\ 0 & 0 & 1 \\ \end{array} \right] \left[ \begin{array}{c} x' \\ y' \\ z' \\ \end{array} \right] \]
- from optical world ( \(x', y', z'\)) to pixel world (\(x, y, z\))
- \(\alpha_{x}, \alpha_{y}\): pixel scaling factor
- \(p_{x}, p_{y}\): principle point
- \(s\): slant factor
3. 3rd Person to 1st Person 3D Mapping (World to Camera)
\[ X_c = \left[ \begin{array}{cc} R_{3 \times 3} & t_{3 \times 1} \\ 0 & 1 \\ \end{array} \right] X \]
World coordinates to camera coordinates
\[ x = K_{3 \times 3} [I; 0]_{3 \times 4} X_c \]
Camera coordinates to pixel coordinates
\[x = K [ R, t ] X\]
Combine 1, 2, 3 here, we have
\[ Z \left[\begin{array}{c} U_{img} \\ V_{img} \\ 1 \\ \end{array}\right] = \left[\begin{array}{ccc} f_x & s & p_x \\ & f_y & p_y \\ & & 1 \\ \end{array}\right] \left[\begin{array}{cccc} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ \end{array}\right] \left[\begin{array}{c} X \\ Y \\ Z \\ 1 \\ \end{array}\right] \]
or
\[ \left[\begin{array}{c} x \\ 1 \\ \end{array}\right] = L \left(\begin{array}{c} K [ R \: t ] \left[\begin{array}{c} X \\ 1 \\ \end{array}\right] \end{array}\right) \]
Camera Calibration
Calibration estimates intrinsic parameters
- \(f\) focal length
- \((u_0, v_0)\) image center
- \(k_1, k_2, \cdots\) radical distortion parameters
Week 3
RANSAC
Problem of Minimum Square Error: outliers will affect result significantly.