最近宾大在 Coursera 上开了一个机器人系列课程，包含了视觉、运动规划、机械设计等课题。我对 SLAM 很感兴趣，于是就选了 Robotics Estimation and Learning 这门课，课程主页是https://www.coursera.org/learn/robotics-learning/。第一周的内容是高斯分布。

一元高斯分布

给定数据集 \(\{x_i\}\)，可以通过最大似然 (Maximum Likelihood Estimate) 来估计均值 \(\mu\) 和标准差 \(\sigma\) \[ \hat{\mu}, \hat{\sigma}=\argmax_{\mu, \sigma}{p(\{x_i\}|\mu, \sigma)} \]

假设所有观测数据独立分布，则有

\[ p(\{x_i\}|\mu, \sigma) = \prod_{i=1}^N p(x_i|\mu, \sigma) \]

解这个优化函数：

\[ \begin{align} \hat{\mu}, \hat{\sigma} &= \argmax_{\mu, \sigma} \prod_{i=1}^N p(x_i|\mu, \sigma) \\ &= \argmax_{\mu, \sigma} \prod_{i=1}^N \ln p(x_i|\mu, \sigma) \\ &= \argmax_{\mu, \sigma} \prod_{i=1}^N \ln (\frac{1}{\sqrt{2\pi}\sigma} \exp(-\frac{(x_i-\mu)^2}{2\sigma^2})) \end{align} \]

设损失函数 \(J(\mu, \sigma) =\sum_{i=1}^N (\frac{(x_i-\mu)^2}{2\sigma^2} + \ln{\sigma})\)，则有 \(\hat{\mu}, \hat{\sigma} = \argmin_{\mu, \sigma} J(\mu, \sigma)\)

\[ \begin{align} \frac{\partial{J}}{\partial{\mu}} &=\frac{\partial{}}{\partial{\mu}}\sum_{i=1}^N (\frac{(x_i-\mu)^2}{2\sigma^2} + \ln{\sigma}) =\sum_{i=1}^N (\frac{\partial{}}{\partial{\mu}}\frac{(x_i-\mu)^2}{2\sigma^2}) \\ \frac{\partial{J}}{\partial{\sigma}} &=\frac{\partial{}}{\partial{\sigma}}\sum_{i=1}^N (\frac{(x_i-\mu)^2}{2\sigma^2} + \ln{\sigma}) =(\frac{\partial}{\partial{\sigma}} \frac{1}{2\sigma^2}) (\sum_{i=1}^N (x_i-\mu)^2) + \frac{N}{\sigma}) \end{align} \]

求极值令两式都为 0，可以解得 \[ \begin{align} \hat{\mu} &= \frac{1}{N} \sum_{i=1}^{N} x_i \\ \hat{\sigma}^2 &= \frac{1}{N} \sum_{i=1}^N (x_i - \hat{\mu})^2 \end{align} \]

多元高斯分布

\[ p(x) = \frac{1}{(2\pi)^{\frac{D}{2}} |\Sigma|^{\frac{1}{2}}} \exp(-\frac{1}{2}(\pmb{x} - \pmb{\mu})^T \Sigma^{-1} (\pmb{x} - \pmb{\mu})) \]

  • \(D\): 维数
  • \(\pmb{X}\): 数据集
  • \(\pmb{\mu}\): 均值向量
  • \(\Sigma\): 协方差矩阵 (covariance matrix)，对角线元素表示方差，非对角线元素表示变量相关性

用最大似然估计多元高斯分布：

\[ \hat{\pmb{\mu}}, \hat{\Sigma}=\argmax_{\pmb{\mu}, \Sigma}{p(\{\pmb{x}_i\}|\pmb{\mu}, \Sigma)} \] 类似于一元高斯分布，假设所有观测独立，则有 \[ \begin{align} \hat{\pmb{\mu}}, \hat{\Sigma} &= \argmax_{\pmb{\mu}, \Sigma} \prod{p(\pmb{x}_i|\pmb{\mu}, \Sigma)} \\ &= \argmax_{\pmb{\mu}, \sigma} \prod_{i=1}^N \ln p(x_i|\pmb{\mu}, \sigma) \\ &= \argmax_{\pmb{\mu}, \sigma} \sum_{i=1}^N (-\frac{1}{2}(\pmb{x}_i - \pmb{\mu})^T \Sigma^{-1} (\pmb{x}_i - \pmb{\mu}) - \frac{1}{2}\ln |\Sigma| + C) \\ &= \argmin_{\pmb{\mu}, \sigma} \sum_{i=1}^N (\frac{1}{2}(\pmb{x}_i - \pmb{\mu})^T \Sigma^{-1} (\pmb{x}_i + \pmb{\mu}) + \frac{1}{2}\ln |\Sigma|) \end{align} \]

设损失函数 \(J(\pmb{\mu, \Sigma}) = \sum_{i=1}^N (\frac{1}{2}(\pmb{x}_i - \pmb{\mu})^T \Sigma^{-1} (\pmb{x}_i + \pmb{\mu}) + \frac{1}{2}\ln |\Sigma|))\)，用类似估计一元高斯分布的方法，令 \(\frac{\partial{J}}{\partial{\pmb{\mu}}}\) 和 \(\frac{\partial{J}}{\partial{\Sigma}}\) 为 0，可以解得 \[ \begin{align} \hat{\pmb{\mu}} &= \frac{1}{N} \sum_{i=1}^{N} \pmb{x}_i \\ \hat{\Sigma} &= \frac{1}{N} \sum_{i=1}^N (\pmb{x}_i - \hat{\pmb{\mu}})(\pmb{x}_i - \hat{\pmb{\mu}})^T \end{align} \]

高斯混合模型 (Gaussian Mixture Model)

GMM 就是多个高斯模型的加权和：

\[ p(x) = \sum_{k=1}^K w_k g_k (\pmb{x}|\pmb{u}_k, \Sigma_k) \]

  • \(g_k\): 单个高斯分布函数
  • \(w_k\): 权值函数，总和为 1

解 GMM 的方法之一就是 EM (Expectation-Maximization)。

EM 法解 GMM

引入隐含变量 \[ z_k^i = \frac{g_k(\pmb{x}_i) | \pmb{u}_k, \Sigma_k}{\sum_{k=1}^K g_k(\pmb{x}_i) | \pmb{u}_k, \Sigma_k} \]

\(z_k^i\) 的表示第 i 个观测数据中，第 k 个高斯函数占全体的比重，直观表示如下图

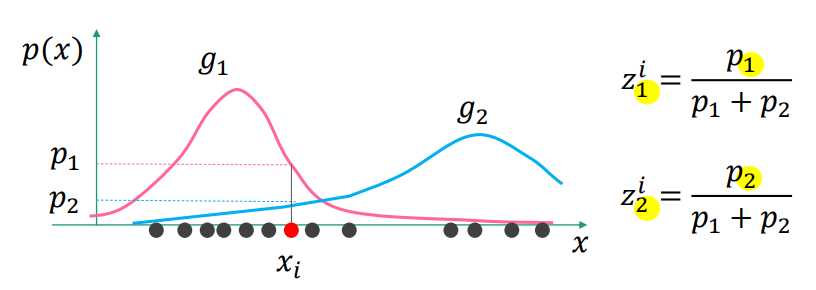z_k^i 的直观表示
\(z_k^i\) 的直观表示

均值向量和协方差矩阵可以通过 \(z_k\) 估计 \[ \begin{align} \hat{\pmb{\mu}}_k &= \frac{1}{z_k} \sum_{i=1}{N} z_k^i \pmb{x}_i \\ \hat{\Sigma}_k &= \frac{1}{z_k} \sum_{i=1}{N} z_k^i (\pmb{x}_i - \hat{\pmb{\mu_k}})(\pmb{x}_i - \hat{\pmb{\mu_k}})^T \\ z_k &= \sum_{i=1}^N z_k^i \end{align} \]

EM 法具体过程

  1. 初始化 \(\pmb{\mu}\) and \(\Sigma\)
  2. 固定 \(\pmb{\mu}\) 和 \(\Sigma\)，并更新 \(z_k^i\) 的值 (E-step)
  3. 固定 \(z_k^i\)，并更新 \(\pmb{\mu}\) 和 \(\Sigma\) 的值 (M-step)
  4. 重复第 2、3 步，直到稳定

全课程的笔记链接