SLAM 公开课笔记 2：卡尔曼滤波

这一周主要讲卡尔曼滤波 (Kalman Filter)，视频讲得比较简略，slides 做得里也有不少错误。最后看了一些其他网站的文章和视频才有了比较深刻的理解。参考资料推荐在本文结尾。

卡尔曼滤波 KF

卡尔曼滤波可以从一系列包含噪音的观测数据中，估计出每个时间点系统的状态。KF 有几个基本假设：

1. 当前状态只和前一状态有关，且和前一状态线性相关，即 $x_{t+1}=A_t{x}_t+B_t{u}_t+{ϵ}_t$，这里 $x_t$ 是状态向量，$u_t$ 为控制向量，${ϵ}_t$ 是均值为 0 的高斯分布噪音。
2. 测量结果和状态线性相关：$z_t=C_t{x}_t+{\delta }_t$。这里 $z_t$ 是测量结果的向量，${\delta }_t$ 表示测量噪音。
3. 最初状态也呈正态分布。

基于高斯分布的假设，我们可以用贝叶斯模型描述状态 $$p\left(x_{t+1}|x_t\right)=Ap\left(x_t\right)p\left(z_t|x_t\right)=Cp\left(x_t\right)$$

加入运动和观测误差导致的不确定性 $v_m$ 和 $v_0$ $$p\left(x_{t+1}|x_t\right)=Ap\left(x_t\right)+v_{m}p\left(z_t|x_t\right)=Cp\left(x_t\right)+v_0$$

假设误差基于高斯分布 $$p\left(x_{t+1}|x_t\right)=AN(x_t,P_t)+N(0,{\Sigma }_m)p\left(z_t|x_t\right)=CN(x_t,P_t)+N(0,{\Sigma }_0)$$

把线性变换 A 和 C 代入正态分布 $$p\left(x_{t+1}|x_t\right)=N(A{x}_t,A{P}_t{A}^T)+N(0,{\Sigma }_m)p\left(z_t|x_t\right)=N(C{x}_t,C{P}_t{C}^T)+N(0,{\Sigma }_0)$$

线性加和 $$p\left(x_{t+1}|x_t\right)=N(A{x}_t,A{P}_t{A}^T+{\Sigma }_m)p\left(z_t|x_t\right)=N(C{x}_t,C{P}_t{C}^T+{\Sigma }_0)$$

接下来讲如何估计这两个高斯分布的参数。

最大后验概率估计卡尔曼滤波

最大后验概率估计的目的在于最大化后验概率 $p\left(x_t|z_t\right)$，即在对 $x_t$ 有一个预测（先验），同时获得了观测结果 $z_t$ 之后修正 $x_t$ 的值，用符号表示有 $\widehat{x_t}={argmax}_{x_t}p\left(x_t|z_t\right)$

由贝叶斯公式 $$p\left(x_t|z_t\right)=\frac{p\left(z_t|x_t\right)p\left(x_t\right)}{P\left(z_t\right)}$$ 代入正态分布得 $$\widehat{x_t}=\underset{x_t}{argmax}N(C{x}_t,{\Sigma }_0)N(A{x}_t,A{P}_t{A}^T+{\Sigma }_m)$$ 令 $$\begin{array}{cc}P& =A{P}_{t-1}{A}^T+{\Sigma }_m\\ R& ={\Sigma }_0\end{array}$$ 代入多元高斯分布（参考第一周笔记）把两个分布合并后求导，或者利用边界条件概率公式，可解得 $$\begin{array}{cc}\widehat{x_t}& =(P^{-1}+C^T{R}^{-1}C{)}^{-1}(C^T{R}^{-1}{Z}_t+P^{-1}A{x}_{t-1})\\ \widehat{P_t}& =(P^{-1}+C^T{R}^{-1}C{)}^{-1}\end{array}$$

接下来根据 Woodbury 矩阵求逆式 (Woodbury Matrix Identity)，可以得到 $$\widehat{P_t}=P-P{C}^T(R^{-1}+CP{C}^T{)}^{-1}CP$$ 令 $K=P{C}^T(R+CP{C}^T{)}^{-1}$，有 $\widehat{P_t}=P-KCP$，$\widehat{x_t}$ 简化过程如下 $$\begin{array}{cc}\widehat{x_t}& =(P^{-1}+C^T{R}^{-1}C{)}^{-1}(C^T{R}^{-1}{z}_t+P^{-1}A{x}_{t-1})\\ & =(P-KCP)(C^T{R}^{-1}{z}_t+P^{-1}A{x}_{t-1})\\ & =A{x}_{t-1}+P{C}^T{R}^{-1}{z}_t-KCA{x}_{t-1}-KCP{C}^T{R}^{-1}{z}_t\\ & =A{x}_{t-1}-KCA{x}_{t-1}+(P{C}^T{R}^{-1}-KCP{C}^T{R}^{-1})z_t\\ & =A{x}_{t-1}-KCA{x}_{t-1}+K{z}_t\end{array}$$

这里 K 就是卡尔曼增益 (Kalman gain)。

扩展卡尔曼滤波 (Extended Kalman Filter)

KF 的局限之一在于假设了线性模型，EKF 去掉了线性模型的限制，可以处理更一般的状态变化函数 $$\begin{array}{cc}{x}_{t+1}=A{x}_t+B{u}_t& =>x_{t+1}=f(x_t,u_k)\\ z_t=C{x}_t& =>z_t=h\left(x_t\right)\end{array}$$

于是协方差的预测变成了 $$p\left(x_{t+1}|x_t\right)=N\left(f\right(x_t),\frac{\partial f}{\partial x}{P}_t\frac{\partial f^T}{\partial x}+{\Sigma }_m)$$ 卡尔曼增益为 $$K=P\frac{\partial h^T}{\partial x}(\frac{\partial h}{\partial x}{P}_t\frac{\partial h^T}{\partial x}{)}^{-1}$$ 更新方程为 $$\begin{array}{cc}\widehat{x_t}& =f\left(x_{t-1}\right)+K(z_t-h(f\left(x_t\right)\left)\right)\\ \widehat{P_t}& =P-K\frac{\partial h}{\partial x}P\end{array}$$

无迹卡尔曼滤波 (Unscented Kalman Filter)

EKF 的局限之一在于只是对非线性的变换做了近似，用泰勒级数展开后取一阶项，容易产生导致较大的误差。UKF 采用了确定性的取样方法来近似高斯分布，这个取样方法又被称为无迹变换 (Unscented Transformation)。

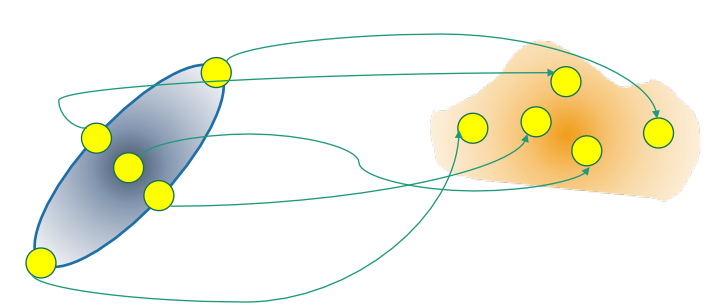
Unscented Transformation

UT 可以用来计算非线形变换后随机变量的分布情况。考虑 L 维随机变量 x 和非线性的函数 $yy=f\left(xx\right)$，假设 x 的均值为 $\overline{xx}$，协方差矩阵 $P_x$。为了计算 $yy$ 的分布情况，我们根据下面三个式子创造一个维数为 2L + 1 的 sigma 矩阵 $XX$： $$\begin{array}{cccc}{X}_0& =\overline{xx}& & \\ X_i& =\overline{xx}+(\sqrt{(L+\lambda )P{P}_x}{)}_i& & i=1,\dots ,L\\ X_i& =\overline{xx}+(\sqrt{(L+\lambda )P{P}_x}{)}_{i-L}& & i=L+1,\dots ,2L\end{array}$$ 这里 $\lambda ={\alpha }^2(L+\kappa )-L$ 为调节参数，$\alpha$ 决定采样点围绕均值的扩散程度等参数。下标 i 表示矩阵的第 i 列。这里的 $X_i$ 也被称为 sigma 向量，通过非线性函数后转变到同一个矩阵中： $$Y_i=f\left(X_i\right)$$

$yy$ 的均值和协方差就可以通过对 $Y$ 矩阵列的加权求和获得了 $$\begin{array}{cc}yy& \approx \sum _{i=0}^{2L}{W}_i^{\left(m\right)}{Y}_i\\ P{P}_y& \approx \sum _{i=0}^{2L}{W}_i^{\left(c\right)}\{Y_i-\overline{yy}\}\{Y_i-\overline{yy}{\}}^T\end{array}$$ 其中权值 $W_i$ 的定义为 $$\begin{array}{ccc}{W}_0^{\left(m\right)}& =\lambda /(L+\lambda )& \\ W_0^{\left(c\right)}& =\lambda /(L+\lambda )+(1-{\alpha }^2+\beta )& \\ W_0^{\left(c\right)}& =W_0^{\left(m\right)}=1/\left\{2\right(L+\lambda \left)\right\}& i=1,\dots ,2L.\end{array}$$ 下图很好地解释了上述几个式子的变换过程

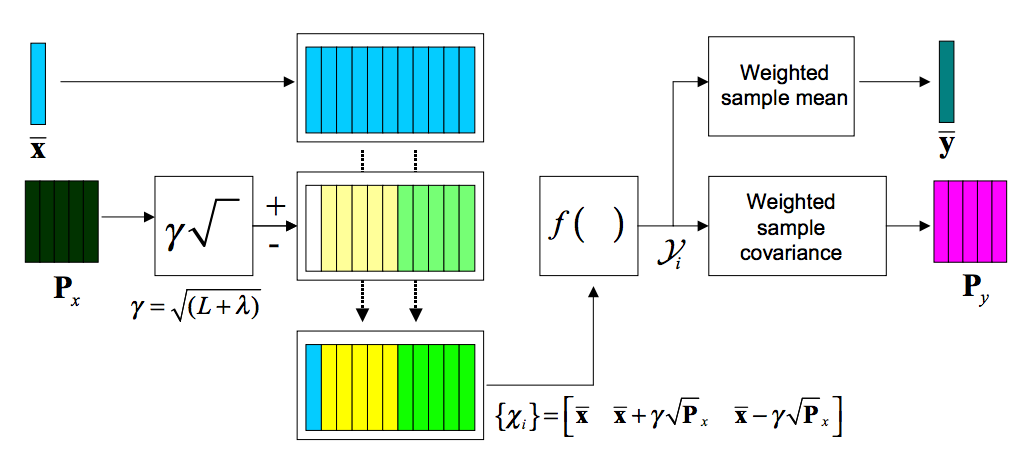
Unscented Kalman Filter

接下来回到 UKF。介绍了 UT 之后 UKF 就容易多了。首先构造一个包含初始状态和噪音的矩阵 $x{x}_k^{\alpha }=[x{x}_k^{T}v{v}_k^{T}n{n}_k^T{]}^T$，这里三个向量分别为状态向量、控制向量和噪音向量。接下来对这个矩阵应用无迹变换获得 sigma 矩阵 $X_k^{\alpha }$，之后就回到了普通 KF 过程。具体的状态转移公式可以参考本文结尾参考资料《Kalman Filtering and Neural Networks》一书中的章节。

作业

这周的作业是用卡尔曼滤波预测一个小球运动 10 帧之后的位置。理解了卡尔曼滤波后做起来不难，定义好动力学矩阵 A 和测量矩阵 C，接着根据上面的公式计算卡尔曼增益 K、新状态的均值和协方差矩阵，再通过新状态的位置和速度计算 10 帧之后的位置就好。

调参方面有一些小技巧，一开始测试的时候可以先给 ${\Sigma }_m$ 设一个很大的值，同时给 ${\Sigma }_0$ 设一个很小的值，这样每次算出来的位置都应该是测量出来的位置，否则代码里可能有 bug。接下来就可以根据生成的预测图来调整 ${\Sigma }_m$，肉眼估一下坐标的误差范围（注意到 y 的变化速度比 x 的慢很多），然后根据坐标误差算一下速度误差。测量误差根据文档可以给一个 0.01 - 0.1 的参数。

参考资料

• How a Kalman filter works, in pictures：这篇是最推荐的，作者还用不同颜色标记各个变量，看起来一目了然。
• Kalman Filter 学习笔记：上文的中文版。
• 《Probabilistic Robotics》一书第三章，pdf 版可以在这里下到。
• Michel van Biezen 的 Kalman Filter 视频：https://youtu.be/CaCcOwJPytQ 比较长，一共有 55 集，但是讲得很细致。
• The Extended Kalman Filter: An Interactive Tutorial for Non-Experts：EKF 的介绍网站，只要求高中数学基础。
• The Unscented Kalman Filter for Nonlinear Estimation: UKF 论文。
• 《Kalman Filtering and Neural Networks》第七章：EKF 和 UKF 的详细介绍。

全课程的笔记链接

• Robotics Estimation and Learning 的课程主页
• 第一周笔记：高斯分布
• 第二周笔记：卡尔曼滤波
• 第三周笔记：地图
• 第四周笔记：定位