最后一周讲定位 (localization)，也就是 SLAM 里面的 L。主要包括粒子滤波和迭代最近点。

里程计定位 (Odometry)

里程计定位法直接从设备里读取信息，更新当前的位置状态。例如要跟踪车子的位置状态，可以在车轮上安装计数器记录车轮转动的次数，从而了解车子前进了多少。对于转弯的情况，可以从内外轮子的计数差得到转弯的角度。假设内轮转了 \(e_i\) 圈，外轮转了 \(e_o\) 圈，内轮半径 \(r_i\)，外轮半径 \(r_o\)，则有 \[ e_i = \theta r_i \\ e_o = \theta r_o \] 这里 \(\theta\) 就是车子转动的角度，上面的方程可以解得 \[ \theta = \frac{e_o - e_i}{r_o - r_i} \] 然后就能根据转动角度更新车辆当前的位置了。

这种方法用车辆本身的坐标系统记录位置，虽然实现起来简单但是测量精度非常局限于测量误差。例如上例中轮子打滑或事漂移都会导致结果不准确。更成熟的方案需要结合地图信息。

地图定位 (Map Registration)

可以用下面三张图来来介绍地图定位问题，左图是当前的区域地图，中间是激光测距传感器得到的结果，地图定位的目的就是根据传感器返回的结果判断机器人当前坐标和朝向，右图就是一个理想的结果。

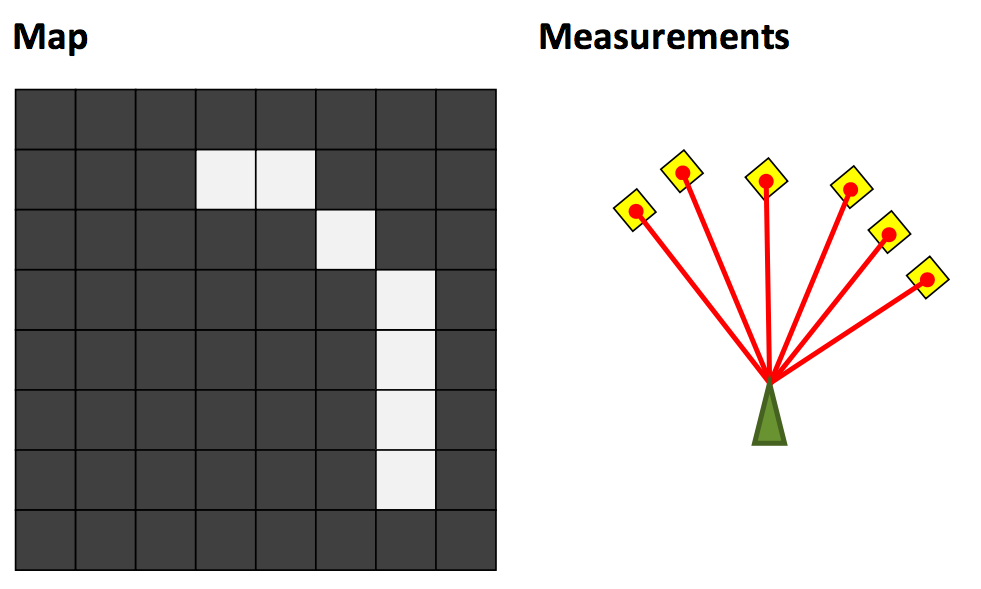
配合第三周讲的占据栅格地图障碍物的概率 \(m(x, y)\)，我们可以定义最佳定位结果应该满足 \[ \max_p \sum_r \delta(p_x + r\cos(p_{\theta} + r_{\theta}), p_y + r\sin(p_{\theta} + r_{\theta})) \cdot{m(x,y)} \] 接下来介绍两种解决地图定位的方法。

粒子滤波 (Particle Filters)

粒子滤波（有没有觉得这个术语的中文翻译很科幻）又称为序列蒙特卡洛 (Sequential Monte Carlo)，是一种非参数 (non-parametric) 模型。它用一系列样本（粒子）表示可能性分布。每一个粒子都是方差接近于 0 的高斯分布，这种分布又被称为狄拉克δ函数 (Dirac Delta)，采用这个分布好处之一是可以把连续数学中的工具应用到离散的结果中。

在地图定位问题中，粒子的状态代表位置和朝向，同时每个粒子分别有自己的权重。初始状态的粒子滤波分布由一开始的假设决定，可能是均匀分布，也可能是以某个点为中心的高斯分布。初始化完成后，重复以下步骤更新粒子的分布：

  1. 根据里程计的信息更新粒子的状态。
  2. 由于里程计本事有不确定，更新每个粒子状态的时候可以加入里程计带入的噪音，通常也是一个高斯分布。
  3. 从每个粒子更新后带噪音的分布中采样。
  4. 根据距离传感器得到的信息，更新每个粒子的权重（例如由传感器得知前方近距离有障碍物，而某个粒子并没有，那么这个粒子的权重都会大幅降低）。
  5. 这样得到的结果可能会有有效粒子过少的问题，需要重新采样。有效粒子的数量可以用 \(n_{effective} = \frac{(\sum_i w_i)^2}{\sum_i w_i^2}\) 表示。
  6. 重新采样的方法就是根据权重重新从粒子集中独立抽取同样数量的粒子，注意这里高权重的粒子可能会被多次抽取。重复抽取的粒子会在下一轮更新时因为里程计噪音再次分散。
  7. 重复步骤，直到粒子集中在某一状态。

迭代最近点 (Iterative Closest Point)

粒子滤波的缺点之一在于高维度中，需要大量的粒子才能保证理想的分布。ICP 算法可以更好的适应高维度的场景。

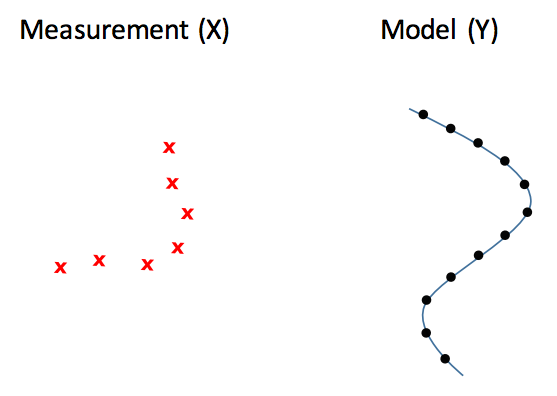
如图所示，ICP 的目的在于已知测量结果和地图，要求出左侧测量结果如何旋转移动后，可以和右侧的地图局部吻合。这里主要有两个问题，一是旋转和移动矩阵，二是测量点和地图点的对应关系。具体的 ICP 算法可以参考这篇论文，它的大致思路和第一周提到的解高斯混合模型的 EM 算法很接近：

  1. 初始化旋转 (R) 和移动 (t) 矩阵。
  2. 固定 R 和 t，优化点的对应关系：\(y_i = \argmin_{y_j \in Y} \Vert x_i - y_j \Vert\)。
  3. 固定点的对应关系，优化 R 和 t：\(R, t = \argmin \sum_{x_i, y_i \in C} \Vert d(x_i, y_i) \Vert ^2\)。
  4. 重复 2 和 3，直到稳定。

作业

这次的作业是实现一个粒子滤波，应该是整个课程最麻烦的一次了。问题本身不算难，尤其简化了动力学模型之后。但是调参比较麻烦，尤其是最后提交的那个地图，容易卡在某个转角跑不出来。

动力学模型方面，我一开始假设机器人位置和朝向的变化量和前一次接近，移动一次粒子之后再添加噪音。这个方法在机器人变向的时候容易位置偏离过多导致粒子失效，后来注意到作业的 Tips 里面建议假设机器人不动，利用高斯噪音移动粒子，这样的话相当于就不需要针对动力学模型做任何操作了。

计算每个例子的得分时，一种做法是用上一周的作业中用到的 bresenham 函数计算发出点到障碍物中间所经历的空白格，然后对每个空白格计算加权，但是这个做法实在太慢了，我最后计算得分时只用了障碍物所在格的状态。

关于粒子的数量，我看到网上有一种做法是设置一个得分的阈值（例如 70% 的障碍物要正好打到墙上），如果所有的粒子都没法超过这个阈值，就重新再跑一次。这么做容易在测量不准时卡死，而且和书中的实现有出入，在现实中会导致粒子滤波每次估计位置时使用的时间不稳定。比较好的做法还是把粒子的数量和高斯分布的参数放在一起调，跑偏了可以看看是因为粒子不够还是分布参数有问题。

作业里其实有两个地图，样例地图比较容易过（可能是参数变化不大）。提交用的地图调参要不少时间，我看了自己的输出以后，发现有几个点的运动变化很大，有可能是这几个点的测量本身也不精确。另外两个地图用来标记墙和空白方格的数值也是不一样的。

小结

至此 Robotics Estimation and Learning 这门课就上完了。课程设置不错，但是讲解不够详细，尤其是第二周和第四周，这小哥讲得太简单了，slides 上还有不少错误。推荐《Probabilistic Robotics》这本书，在上课的时候参考了里面一部分章节，写得很详细，作者 Thrun 也是机器人领域的大神。

全课程的笔记链接